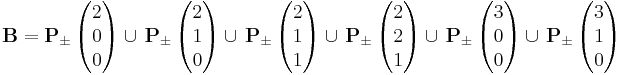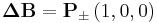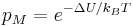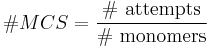Bond fluctuation model

The BFM (bond fluctuation model or bond fluctuation method) is a lattice model for simulating the conformation and dynamics of polymer systems. There are two versions of the BFM used: The earlier version was first introduced by Carmesin and Kremer in 1988^[1], and the later version by Shaffer in 1994 ^[2]. Conversion between models is possible.^[3]

1 Model
- 1.1 Carmesin and Kremer version
- 1.2 Shaffer's version
2 Monte Carlo step
3 Mandatory conditions for Carmesin–Kremer BFM
4 Mandatory conditions for Shaffer BFM
5 Optional conditions
6 Notes
7 External links

Model

Carmesin and Kremer version

In this model the monomers are represented by cubes on a regular cubic lattice with each cube occupying eight lattice positions. Each lattice position can only be occupied by one monomer in order to model excluded volume. The monomers are connected by a bond vector, which is taken from a set of typically 108 allowed vectors. There are different definitions for this vector set. One example for a bond vector set is made up from the six base vectors below using permutation and sign variation of the three vector components in each direction:

$\mathbf{B} = \mathbf{P_\pm} \left( \begin{matrix} 2 \\ 0 \\ 0 \end{matrix} \right) \cup \!\ \mathbf{P_\pm} \left( \begin{matrix} 2 \\ 1 \\ 0 \end{matrix} \right) \cup \!\ \mathbf{P_\pm} \left( \begin{matrix} 2 \\ 1 \\ 1 \end{matrix} \right) \cup \!\ \mathbf{P_\pm} \left( \begin{matrix} 2 \\ 2 \\ 1 \end{matrix} \right) \cup \!\ \mathbf{P_\pm} \left( \begin{matrix} 3 \\ 0 \\ 0 \end{matrix} \right) \cup \!\ \mathbf{P_\pm} \left( \begin{matrix} 3 \\ 1 \\ 0 \end{matrix} \right)$

The resulting bond lengths are 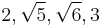$2, \sqrt{5}, \sqrt{6}, 3$ and $\sqrt{10}$ .

The combination of bond vector set and monomer shape in this model ensures that polymer chains cannot cross each other, without explicit test of the local topology.

The basic movement of a monomer cube takes place along the lattice axes

$\mathbf{\Delta B} = \mathbf{P_\pm} \left(1, 0, 0 \right)$

so that each of the possible bond vectors can be realized.^[4]

Shaffer's version

As in the case of the Carmesin-Kremer BFM, the Shaffer BFM is also constructed on a simple-cubic lattice. However, the lattice points, or vertices of each cube are the sites that can be occupied by a monomer. Each lattice point can be occupied by one monomer only. Successive monomers along a polymer backbone are connected by bond vectors. The allowed bond vectors must be one of: (a) A cube edge (b) A face diagonal or (c) A solid diagonal. The resulting bond lengths are 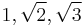$1, \sqrt{2}, \sqrt{3}$ . In addition to the bond length constraint, polymers should not be allowed to cross. This is done most efficiently by the use of a secondary lattice which is twice as fine as the original lattice. The secondary lattice tracks the mid-points of the bonds in the system, and forbids the overlap of bond midpoints. This effectively leads to disallowing polymers from crossing each other.

Monte Carlo step

In both versions of the BFM, a single attempt to move one monomer consists of the following steps which are standard for Monte Carlo methods:

Select a monomer m and a direction 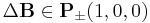$\Delta \mathbf{B} \in \mathbf{P}_\pm(1,0,0)$ randomly
Check list of conditions (see below)
If all conditions are fulfilled, perform move

The conditions to perform a move can be subdivided into mandatory and optional ones.

Mandatory conditions for Carmesin–Kremer BFM

Four lattice sites next to monomer m in the direction d are empty
The move does not lead to bonds that are not contained in the bond vector set.

Mandatory conditions for Shaffer BFM

The lattice site to which the chosen monomer is going to be moved is empty
The move does not lead to bonds that are not contained in the bond vector set.
The move does not lead to overlapping of bond mid-points.

Optional conditions

If the move leads to an energetic difference 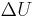$\Delta U$ for example due to an electric field or an adsorbing force to the walls. In this case a Metropolis algorithm is applied: The Metroplis rate 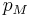$p_M$ which is defined as